Analyse Statistique
MessagePosté: Lun Mar 22, 2010 3:45 pm
Une mauvaise interprétation des chiffres revient à prendre en compte une fausse information, ce qui peut être pire que de rien mesurer.
Etre critique sur le contexte
Tout chiffre doit être regardé en prenant en compte le cadre de mesure expérimental.
Il peut toujours y avoir quelque chose qui influence les chiffres observés, dès fois, c'est même carrément
le contexte qui explique les résultats observés.
EXEMPLES :
- Vous menez un test d'acquisition d'abonnés, vous testez une nouvelle version en parallèle de votre version de référence.
Si votre nouvelle version fait une nouvelle offre, et que vos abonnés existant peuvent la voir, il y a de fortes chances que la
curiosité les emporte et qu'ils y adhèrent. La même remarque vaut pour des visiteurs qui reviennent naturellement, ce genre
de test ne devrait porter que sur des visiteurs qui vous découvrent la première fois.
- Vous comparez des taux de clic ou de transformation entre les messages d'une séquence, s'il y a une suite logique entre les messages,
il y aura une logique dans les résultats. Sur Cybermailing, par exemple, nous proposons un cours gratuit en vidéo sur le marketing par email.
Les messages qui induisent le plus de ventes sont le premier et le dernier, cela signifie t'il qu'ils sont plus performants que les messages
intermédiaires ? Non, le premier message suffit à mettre en confiance ceux qui voulaient agir rapidement, et le dernier termine la séquence
d'informations, il est logique qu'une bonne partie attende la fin de cette séquence pour agir.
Ce qu'il faut retenir de ce point, c'est que le cadre d'une expérience doit être choisi au mieux pour que les différences observées
soient bien dû aux paramètres que l'on souhaite observer et pas à autre chose.
Validité Statistique
Si vous comparez les résultats d'un test et que vous observez 10 réalisations pour l'un et 15 pour l'autre, lequel est le meilleur ?
Laissez moi prendre un "dé" pour vous montrer que la réponse n'est pas aussi simple qu'il n'y paraît...
Un dé à jouer classique a 6 faces. Donc lorsque vous le lancez, chaque face à 1 chance sur 6 de sortir soit 16.666% de chance.
Une page d'inscription qui aurait un taux d'inscription de 16.666% se comporte alors comme un "dé" à 6 faces qui serait lancé par vos visiteurs
et vous obtenez l'inscription seulement s'ils sortent un 6.
Maintenant, Didier a un beau dé rouge, et moi un dé bleu, et il prétend qu'il donne plus facilement des 6 que le mien.
Que cela ne tienne, nous entrons dans une compétition de dé, celui qui fera le plus de 6 pour le même nombre de lancers.
Au 1er lancer, Didier fait un 6, Lionel non
Au 2e lancer aucun ne fait 6
Au 3e lancer, Didier fait un 6, Lionel non
Au 4e lancer, Didier fait un 6, Lionel non - wow ! aurait-il un super dé ?
.. Au bout de 10 lancers, Lionel se rattrape avec des 6 obtenus aux tirages 7 et 9, Didier n'améliore pas.
Nous faisons les comptes 20% de réussite pour Lionel et 30 % pour Didier.
Nos dés semblent meilleurs que de nature (supérieurs à 16.6666%) et Didier aurait bien un dé meilleur que celui de Lionel.

Mais Lionel est scientifique et il décide de pousser l'expérience beaucoup plus loin et ils réalisent chacun 450 tirages !
Lionel enregistre les résultats, compile les taux de réussite et en fait un graphique :
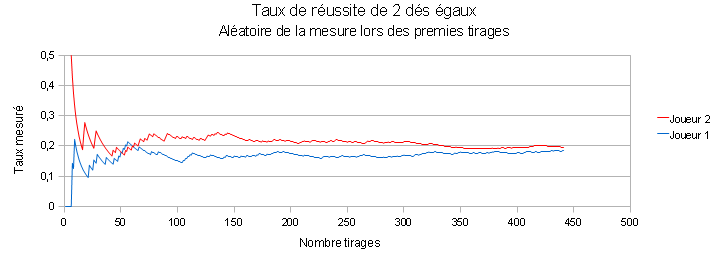
Le dé de Didier semble toujours meilleur mais la différence semble s'atténuer... que penser ?
En réalité, les dés sont égaux, et les différences observées ne sont que le fait du hasard !
En vérité, nous n'avons même pas joué au dé, j'ai juste programmé un tirage aléatoire avec une chance de réussite de 16.6666% dans le tableur de open office.
Si vous voulez jouer avec :
téléchargez la version Open Office
ou
téléchargez la version Excel
Vous pourrez même changer le taux de réussite pour voir ce qui se passe.
En fait, cette expérience n'illustre qu'une seule chose : les différences mesurées ne sont statistiquement pas significatives !
Mais alors comment pouvons nous savoir, lorsque nous observons les résultats d'un test qui indique que A est meilleur que B
si les résultats observés sont significatifs ?
La réponse est : "vous ne pouvez jamais savoir" !
Cependant les statistiques disposent de formules qui peuvent nous venir en aide car si vous ne pouvez jamais être sur à 100% que vos résultats sont significatifs, vous pouvez par exemple savoir qu'ils le sont avec 95% de chance de ne pas vous tromper (c'est à dire 5% de vous tromper..)
Les statisticiens appellent cela la vérification de l'hypothèse "nulle", qui consiste à savoir si les résultats observés sont le fruit du hasard ou non.
Mais comme souvent en statistique, il n'y a pas de réponse tranchée, ils ne peuvent vérifier l'hypothèse nulle qu'en l'associant à un niveau de confiance.
La plupart des études statistiques (politique, économique, médicale) se basent sur un niveau de confiance de 95%, qui signifie que les données sont considérées comme significatives lorsqu'il n'y a plus que 5% de chance que les écarts observés ne soient en fait que le pur fruit du hasard.
Mais ce chiffre de 95%, comme vous le verrez plus bas, nécessite en général une quantité de données bien difficiles à acquérir, et il peut être plus judicieux à un chef d'entreprise, d'être capable de prendre des décisions avec un niveau de confiance moins élévé...
En fait vous pouvez calculer un intervalle de confiance de vos mesures, et en déduire quel pourcentage de chance vous avez que A soit réellement meilleur que B.
C'est ce que fait ce fichier excel calcul du niveau de confiance.
Vous y entrez des résultats de test et il calcule le niveau de confiance.
En faisant varier les chiffres en bleu de ce fichier, vous découvrirez les tendances suivantes :
- Plus le nombre d'échantillons est grand, plus le niveau de confiance augmente (ce n'est pas une nouvelle...)
- Plus les différences entre A et B sont importantes, plus le niveau de confiance est elevé
Mais aussi
- Plus le taux de conversion est élevé, plus il est facile d'observer des résultats significatifs.
Illustration :
Pour constater une amélioration de 10% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 3 200 échantillons
Pour un taux de conversion de référence de 25 % : 9 600 échantillons
Pour un taux de conversion de référence de 10 % : 30 000 échantillons
Pour un taux de conversion de référence de 1 % : 320 000 échantillons !
Pour constater une amélioration de 10% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 1 400 échantillons
Pour un taux de conversion de référence de 25 % : 4 200 échantillons
Pour un taux de conversion de référence de 10 % : 13 000 échantillons
Pour un taux de conversion de référence de 1 % : 140 000 échantillons !
Pour constater une amélioration de 25% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 480 échantillons
Pour un taux de conversion de référence de 25 % : 1 600 échantillons
Pour un taux de conversion de référence de 10 % : 6 000 échantillons
Pour un taux de conversion de référence de 1 % : 58 000 échantillons !
Pour constater une amélioration de 25% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 210 échantillons
Pour un taux de conversion de référence de 25 % : 700 échantillons
Pour un taux de conversion de référence de 10 % : 2 200 échantillons
Pour un taux de conversion de référence de 1 % : 24 000 échantillons !
Pour constater une amélioration de 50% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 108 échantillons
Pour un taux de conversion de référence de 25 % : 420 échantillons
Pour un taux de conversion de référence de 10 % : 960 échantillons
Pour un taux de conversion de référence de 1 % : 15 600 échantillons !
Pour constater une amélioration de 50% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 46 échantillons
Pour un taux de conversion de référence de 25 % : 180 échantillons
Pour un taux de conversion de référence de 10 % : 580 échantillons
Pour un taux de conversion de référence de 1 % : 6 600 échantillons !
Les conséquences pratiques de cette observation sont multiples :
Parmi les plus évidentes j'évoquerai que :
- A moins de disposer d'une quantité phénoménale de données, vous ne serez pas capable de distinguer une faible augmentation d'un faible taux.
Sur un faible taux, vous ne pouvez espérer observer que des améliorations (ou détériorations phénoménales)
- Vous avez tout intérêt à focaliser vos tests et vos analyses sur les éléments qui ont déjà des taux élevés, les observations vont beaucoup plus vite.
Cela revient à s'intéresser aux processus intermédiaires de votre conversion. Une conversion globale étant en génréral composée de plusieurs étapes,
vous veillerez à améliorer les rendements de chacune des étapes.
- Avez vous besoin de 95% de certitude que votre décision ne se base pas sur le hasard ?
Il me semble que non.
Avec 80% de certitude, vous agissez 8 fois sur 10 sur la base de résultats observés, et 2 fois sur 10 au hasard.
Quand vous agissez au hasard, certes vos mesures ne vous servent à rien, mais vous ne prenez pas systématiquement la mauvaise direction.
En simplifiant, agissant avec 80% de niveau de confiance, vous faites probablement le bon choix 9 fois sur 10.. ce qui semble très raisonnable.
A la limite, ceux qui aiment le risque peuvent agir avec 50% de confiance. Ce qui signifie que seul un test sur deux valait la peine d'être fait et
que pour les autres, bien qu'ils étaient fait, la décision prise ne prend pas en compte le résultat...
- Pour finir, méfiez-vous toujours des résultats basés sur peu de conversions (10 semble être un grand minium, 100 est bien meilleur).
Les formules statistiques donnent des résultats dans tous les cas, mais leur validité mathématique suppose toujours un grand nombre de données.
Donc quand vous en avez peu, les formules ne sont pas nécéssairements justes...
Etre critique sur le contexte
Tout chiffre doit être regardé en prenant en compte le cadre de mesure expérimental.
Il peut toujours y avoir quelque chose qui influence les chiffres observés, dès fois, c'est même carrément
le contexte qui explique les résultats observés.
EXEMPLES :
- Vous menez un test d'acquisition d'abonnés, vous testez une nouvelle version en parallèle de votre version de référence.
Si votre nouvelle version fait une nouvelle offre, et que vos abonnés existant peuvent la voir, il y a de fortes chances que la
curiosité les emporte et qu'ils y adhèrent. La même remarque vaut pour des visiteurs qui reviennent naturellement, ce genre
de test ne devrait porter que sur des visiteurs qui vous découvrent la première fois.
- Vous comparez des taux de clic ou de transformation entre les messages d'une séquence, s'il y a une suite logique entre les messages,
il y aura une logique dans les résultats. Sur Cybermailing, par exemple, nous proposons un cours gratuit en vidéo sur le marketing par email.
Les messages qui induisent le plus de ventes sont le premier et le dernier, cela signifie t'il qu'ils sont plus performants que les messages
intermédiaires ? Non, le premier message suffit à mettre en confiance ceux qui voulaient agir rapidement, et le dernier termine la séquence
d'informations, il est logique qu'une bonne partie attende la fin de cette séquence pour agir.
Ce qu'il faut retenir de ce point, c'est que le cadre d'une expérience doit être choisi au mieux pour que les différences observées
soient bien dû aux paramètres que l'on souhaite observer et pas à autre chose.
Validité Statistique
Si vous comparez les résultats d'un test et que vous observez 10 réalisations pour l'un et 15 pour l'autre, lequel est le meilleur ?
Laissez moi prendre un "dé" pour vous montrer que la réponse n'est pas aussi simple qu'il n'y paraît...
Un dé à jouer classique a 6 faces. Donc lorsque vous le lancez, chaque face à 1 chance sur 6 de sortir soit 16.666% de chance.
Une page d'inscription qui aurait un taux d'inscription de 16.666% se comporte alors comme un "dé" à 6 faces qui serait lancé par vos visiteurs
et vous obtenez l'inscription seulement s'ils sortent un 6.
Maintenant, Didier a un beau dé rouge, et moi un dé bleu, et il prétend qu'il donne plus facilement des 6 que le mien.
Que cela ne tienne, nous entrons dans une compétition de dé, celui qui fera le plus de 6 pour le même nombre de lancers.
Au 1er lancer, Didier fait un 6, Lionel non
Au 2e lancer aucun ne fait 6
Au 3e lancer, Didier fait un 6, Lionel non
Au 4e lancer, Didier fait un 6, Lionel non - wow ! aurait-il un super dé ?
.. Au bout de 10 lancers, Lionel se rattrape avec des 6 obtenus aux tirages 7 et 9, Didier n'améliore pas.
Nous faisons les comptes 20% de réussite pour Lionel et 30 % pour Didier.
Nos dés semblent meilleurs que de nature (supérieurs à 16.6666%) et Didier aurait bien un dé meilleur que celui de Lionel.

Mais Lionel est scientifique et il décide de pousser l'expérience beaucoup plus loin et ils réalisent chacun 450 tirages !
Lionel enregistre les résultats, compile les taux de réussite et en fait un graphique :

Le dé de Didier semble toujours meilleur mais la différence semble s'atténuer... que penser ?
En réalité, les dés sont égaux, et les différences observées ne sont que le fait du hasard !
En vérité, nous n'avons même pas joué au dé, j'ai juste programmé un tirage aléatoire avec une chance de réussite de 16.6666% dans le tableur de open office.
Si vous voulez jouer avec :
téléchargez la version Open Office
ou
téléchargez la version Excel
Vous pourrez même changer le taux de réussite pour voir ce qui se passe.
En fait, cette expérience n'illustre qu'une seule chose : les différences mesurées ne sont statistiquement pas significatives !
Mais alors comment pouvons nous savoir, lorsque nous observons les résultats d'un test qui indique que A est meilleur que B
si les résultats observés sont significatifs ?
La réponse est : "vous ne pouvez jamais savoir" !
Cependant les statistiques disposent de formules qui peuvent nous venir en aide car si vous ne pouvez jamais être sur à 100% que vos résultats sont significatifs, vous pouvez par exemple savoir qu'ils le sont avec 95% de chance de ne pas vous tromper (c'est à dire 5% de vous tromper..)
Les statisticiens appellent cela la vérification de l'hypothèse "nulle", qui consiste à savoir si les résultats observés sont le fruit du hasard ou non.
Mais comme souvent en statistique, il n'y a pas de réponse tranchée, ils ne peuvent vérifier l'hypothèse nulle qu'en l'associant à un niveau de confiance.
La plupart des études statistiques (politique, économique, médicale) se basent sur un niveau de confiance de 95%, qui signifie que les données sont considérées comme significatives lorsqu'il n'y a plus que 5% de chance que les écarts observés ne soient en fait que le pur fruit du hasard.
Mais ce chiffre de 95%, comme vous le verrez plus bas, nécessite en général une quantité de données bien difficiles à acquérir, et il peut être plus judicieux à un chef d'entreprise, d'être capable de prendre des décisions avec un niveau de confiance moins élévé...
En fait vous pouvez calculer un intervalle de confiance de vos mesures, et en déduire quel pourcentage de chance vous avez que A soit réellement meilleur que B.
C'est ce que fait ce fichier excel calcul du niveau de confiance.
Vous y entrez des résultats de test et il calcule le niveau de confiance.
En faisant varier les chiffres en bleu de ce fichier, vous découvrirez les tendances suivantes :
- Plus le nombre d'échantillons est grand, plus le niveau de confiance augmente (ce n'est pas une nouvelle...)
- Plus les différences entre A et B sont importantes, plus le niveau de confiance est elevé
Mais aussi
- Plus le taux de conversion est élevé, plus il est facile d'observer des résultats significatifs.
Illustration :
Pour constater une amélioration de 10% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 3 200 échantillons
Pour un taux de conversion de référence de 25 % : 9 600 échantillons
Pour un taux de conversion de référence de 10 % : 30 000 échantillons
Pour un taux de conversion de référence de 1 % : 320 000 échantillons !
Pour constater une amélioration de 10% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 1 400 échantillons
Pour un taux de conversion de référence de 25 % : 4 200 échantillons
Pour un taux de conversion de référence de 10 % : 13 000 échantillons
Pour un taux de conversion de référence de 1 % : 140 000 échantillons !
Pour constater une amélioration de 25% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 480 échantillons
Pour un taux de conversion de référence de 25 % : 1 600 échantillons
Pour un taux de conversion de référence de 10 % : 6 000 échantillons
Pour un taux de conversion de référence de 1 % : 58 000 échantillons !
Pour constater une amélioration de 25% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 210 échantillons
Pour un taux de conversion de référence de 25 % : 700 échantillons
Pour un taux de conversion de référence de 10 % : 2 200 échantillons
Pour un taux de conversion de référence de 1 % : 24 000 échantillons !
Pour constater une amélioration de 50% d'un taux de conversion avec un niveau de confiance de 95 %, il faut :
Pour un taux de conversion de référence de 50 % : 108 échantillons
Pour un taux de conversion de référence de 25 % : 420 échantillons
Pour un taux de conversion de référence de 10 % : 960 échantillons
Pour un taux de conversion de référence de 1 % : 15 600 échantillons !
Pour constater une amélioration de 50% d'un taux de conversion avec un niveau de confiance de 80 %, il faut :
Pour un taux de conversion de référence de 50 % : 46 échantillons
Pour un taux de conversion de référence de 25 % : 180 échantillons
Pour un taux de conversion de référence de 10 % : 580 échantillons
Pour un taux de conversion de référence de 1 % : 6 600 échantillons !
Les conséquences pratiques de cette observation sont multiples :
Parmi les plus évidentes j'évoquerai que :
- A moins de disposer d'une quantité phénoménale de données, vous ne serez pas capable de distinguer une faible augmentation d'un faible taux.
Sur un faible taux, vous ne pouvez espérer observer que des améliorations (ou détériorations phénoménales)
- Vous avez tout intérêt à focaliser vos tests et vos analyses sur les éléments qui ont déjà des taux élevés, les observations vont beaucoup plus vite.
Cela revient à s'intéresser aux processus intermédiaires de votre conversion. Une conversion globale étant en génréral composée de plusieurs étapes,
vous veillerez à améliorer les rendements de chacune des étapes.
- Avez vous besoin de 95% de certitude que votre décision ne se base pas sur le hasard ?
Il me semble que non.
Avec 80% de certitude, vous agissez 8 fois sur 10 sur la base de résultats observés, et 2 fois sur 10 au hasard.
Quand vous agissez au hasard, certes vos mesures ne vous servent à rien, mais vous ne prenez pas systématiquement la mauvaise direction.
En simplifiant, agissant avec 80% de niveau de confiance, vous faites probablement le bon choix 9 fois sur 10.. ce qui semble très raisonnable.
A la limite, ceux qui aiment le risque peuvent agir avec 50% de confiance. Ce qui signifie que seul un test sur deux valait la peine d'être fait et
que pour les autres, bien qu'ils étaient fait, la décision prise ne prend pas en compte le résultat...
- Pour finir, méfiez-vous toujours des résultats basés sur peu de conversions (10 semble être un grand minium, 100 est bien meilleur).
Les formules statistiques donnent des résultats dans tous les cas, mais leur validité mathématique suppose toujours un grand nombre de données.
Donc quand vous en avez peu, les formules ne sont pas nécéssairements justes...